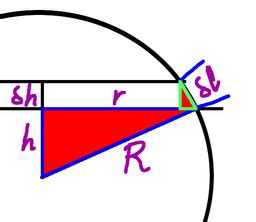
archimedes hat-box theorem uniform sphere distribution Archimedes' Theorem says axial projection of any measurable region on a sphere on the right circular cylinder circumscribed about the sphere preserves area. picture from Archimedes' Hat . Around the time your house was built an electrical equipment manufacture in NY developed greenfield flexible conduit and then later while experimenting with pre-installing wire in it .
0 · sphere hat box theorem
1 · hat box theorem
2 · archimedes hat box
Find company research, competitor information, contact details & financial data for W.H.S. Sheet Metal Ltd. of North York, ON. Get the latest business insights from Dun & Bradstreet.
Abstract. Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present .
Archimedes’ hat-box theorem states that uniform measure ona sphere projects to uniform measure on an interval. This fact can be used to derive Simpson’s rule. Archimedes' Hat-Box Theorem Enclose a sphere in a cylinder and cut out a spherical segment by slicing twice perpendicularly to the cylinder 's axis. Then the lateral surface area of the spherical segment is equal to the lateral . Let ${\bf u} \in \mathbb{R}^3$ be a random vector with uniform distribution on the three-dimensional unit sphere. Then the projection on any given unit vector $\bf v \in .Archimedes' Theorem says axial projection of any measurable region on a sphere on the right circular cylinder circumscribed about the sphere preserves area. picture from Archimedes' Hat .
Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various .
sphere hat box theorem
hat box theorem
Since the unique rotation-invariant distribution on the surface of a sphere of any dimension is the uniform dis-tribution (Theorem 4.1.2 of [6]), the propositions of Archimedes and Herschel . Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present .U has the uniform distribution on the sphere. That means that if E is any subset of S, then the probability such that U falls into E is proportional to the area A ( E ) of E .Theorem (Archimedes) Let f : S2!R be given by (x;y;z) 7!z. Then the pushforward of the standard measure on the sphere to the interval is 2ˇ times Lebesgue measure. arXiv:math/0405366v2 .
Abstract. Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.Archimedes’ hat-box theorem states that uniform measure ona sphere projects to uniform measure on an interval. This fact can be used to derive Simpson’s rule. Archimedes' Hat-Box Theorem Enclose a sphere in a cylinder and cut out a spherical segment by slicing twice perpendicularly to the cylinder 's axis. Then the lateral surface area of the spherical segment is equal to the lateral surface area cut out of the cylinder by the same slicing planes, i.e.,

Let ${\bf u} \in \mathbb{R}^3$ be a random vector with uniform distribution on the three-dimensional unit sphere. Then the projection on any given unit vector $\bf v \in \mathbb{R}^3$ $$X = {\bf u}^\mathrm{T} {\bf v}$$ has uniform distribution $$X .Archimedes' Theorem says axial projection of any measurable region on a sphere on the right circular cylinder circumscribed about the sphere preserves area. picture from Archimedes' Hat-Box Theorem. Enclose a sphere in a cylinder and cut out a spherical segment by slicing perpendicularly to the cylinder's axis.
archimedes hat box
Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.Since the unique rotation-invariant distribution on the surface of a sphere of any dimension is the uniform dis-tribution (Theorem 4.1.2 of [6]), the propositions of Archimedes and Herschel-Maxwell suggest the following characterization of mean-zero Gaussian distributions; we provide a proof and discussion of generalizations in the last section.
Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.U has the uniform distribution on the sphere. That means that if E is any subset of S, then the probability such that U falls into E is proportional to the area A ( E ) of E .Theorem (Archimedes) Let f : S2!R be given by (x;y;z) 7!z. Then the pushforward of the standard measure on the sphere to the interval is 2ˇ times Lebesgue measure. arXiv:math/0405366v2 [math.NA] 22 Sep 2004 Numerical cubature from ArchimedesÕ hat-box theorem Greg Kuperberg! Department of Mathematics, University of California, Davis, CA 95616Abstract. Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.
precision metal fabrication manufacturers
Archimedes’ hat-box theorem states that uniform measure ona sphere projects to uniform measure on an interval. This fact can be used to derive Simpson’s rule. Archimedes' Hat-Box Theorem Enclose a sphere in a cylinder and cut out a spherical segment by slicing twice perpendicularly to the cylinder 's axis. Then the lateral surface area of the spherical segment is equal to the lateral surface area cut out of the cylinder by the same slicing planes, i.e., Let ${\bf u} \in \mathbb{R}^3$ be a random vector with uniform distribution on the three-dimensional unit sphere. Then the projection on any given unit vector $\bf v \in \mathbb{R}^3$ $$X = {\bf u}^\mathrm{T} {\bf v}$$ has uniform distribution $$X .Archimedes' Theorem says axial projection of any measurable region on a sphere on the right circular cylinder circumscribed about the sphere preserves area. picture from Archimedes' Hat-Box Theorem. Enclose a sphere in a cylinder and cut out a spherical segment by slicing perpendicularly to the cylinder's axis.
Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.Since the unique rotation-invariant distribution on the surface of a sphere of any dimension is the uniform dis-tribution (Theorem 4.1.2 of [6]), the propositions of Archimedes and Herschel-Maxwell suggest the following characterization of mean-zero Gaussian distributions; we provide a proof and discussion of generalizations in the last section. Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.
U has the uniform distribution on the sphere. That means that if E is any subset of S, then the probability such that U falls into E is proportional to the area A ( E ) of E .
As stated above, a blinking red light on circuit breaker signals that it has tripped due to inconsistent or other abnormal electrical flow within our circuits. Or worse, a red light means that the breaker has blown due to the amount of electricity it has .
archimedes hat-box theorem uniform sphere distribution|archimedes hat box