binomial distribution bayes box for p Expected value and varianceIf X ~ B(n, p), that is, X is a binomially distributed random variable, n being the total number of experiments and p the probability of each . See more
Two homes, both painted white with black trim, could look entirely different. Make sure to explore the possibilities to find the perfect hues for your design vision! Take a peek at THD-6607, a beautiful modern farmhouse with a charcoal black shingle and metal roof.
0 · wikipedia binomial distribution
1 · example of a binomial distribution
2 · binomial distribution without replacement
3 · binomial distribution statistics
4 · binomial distribution probability
5 · binomial distribution in math
6 · beta and binomial distribution
7 · bayes rule binomial proportion
Example of a beach style green two-story mixed siding house exterior design in Jacksonville with a hip roof, a metal roof and a white roof
Probability mass function If the random variable X follows the binomial distribution with parameters n ∈ $${\displaystyle \mathbb {N} }$$ and p ∈ [0, 1], we write X ~ B(n, p). The probability of getting exactly k successes in n independent Bernoulli trials (with the same rate p) is given by the probability mass function: . See more
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a See more
wikipedia binomial distribution
example of a binomial distribution
Estimation of parametersWhen n is known, the parameter p can be estimated using the proportion of successes: See moreRandom number generationMethods for random number generation where the marginal distribution is a binomial distribution . See more• Mathematics portal• Logistic regression• Multinomial distribution• Negative binomial distribution• Beta-binomial distribution See moreExpected value and varianceIf X ~ B(n, p), that is, X is a binomially distributed random variable, n being the total number of experiments and p the probability of each . See more
Sums of binomialsIf X ~ B(n, p) and Y ~ B(m, p) are independent binomial variables with the same probability p, . See moreThis distribution was derived by Jacob Bernoulli. He considered the case where p = r/(r + s) where p is the probability of success and r and s are positive integers. Blaise Pascal had . See more The following function computes the binomial distribution for given values of n and p: def make_binomial ( n , p ): """Make a binomial PMF. n: number of spins p: probability of heads returns: Series representing a PMF """ .As we build up the equations, we'll put them together to create a generalized function for the binomial distribution. ***::: {#thm-permuation-example} #### Permuation Example for the .
Find the joint distribution of \(p\) and \(X\). Use R to simulate a sample of size 1000 from the joint distribution of \((p, X)\). From inspecting a histogram of the simulated values of \(X\), guess at .We will denote our posterior distribution for θ using p(θ|Y ). The likelihood function L(θ|Y ) is a function of θ that shows how “likely” are various parameter values θ to have produced the data .For n = 1, the binomial distribution becomes the Bernoulli distribution. The mean value of a Bernoulli variable is = p, so the expected number of S’s on any single trial is p.
More generally, suppose the probability of heads is p and we spin the coin n times. The probability that we get a total of k heads is given by the binomial distribution: for any value of k from 0 to n, including both. The term (n .We now have two pieces of our Bayesian model in place – the Beta prior model for Michelle’s support \(\pi\) and the Binomial model for the dependence of polling data \(Y\) on \(\pi\): \[\begin{split} Y | \pi & \sim \text{Bin}(50, \pi) \ \pi & \sim . Bayesian Inference is the use of Bayes theorem to estimate parameters of an unknown probability distribution. The framework uses data to update model beliefs, i.e., the distribution over the parameters of the model.
The binomial distribution is the PMF of k successes given n independent events each with a probability p of success. Mathematically, when α = k + 1 and β = n − k + 1, the beta distribution and the binomial distribution are related by [clarification needed] a factor of n + 1: The following function computes the binomial distribution for given values of n and p: def make_binomial ( n , p ): """Make a binomial PMF. n: number of spins p: probability of heads returns: Series representing a PMF """ ks = np . arange ( n + 1 ) a = binom . .In Bayes' rule above we can see that the posterior distribution is proportional to the product of the prior distribution and the likelihood function: \begin{eqnarray} P(\theta | D) \propto P(D|\theta) P(\theta) \end{eqnarray}As we build up the equations, we'll put them together to create a generalized function for the binomial distribution. ***::: {#thm-permuation-example} #### Permuation Example for the Binomial Distribution - Each outcome we care about will have the *same* probability.
binomial distribution without replacement
Find the joint distribution of \(p\) and \(X\). Use R to simulate a sample of size 1000 from the joint distribution of \((p, X)\). From inspecting a histogram of the simulated values of \(X\), guess at the marginal distribution of \(X\). R Exercises. Simulating Multinomial Probabilities; Revisit Exercise 6.We will denote our posterior distribution for θ using p(θ|Y ). The likelihood function L(θ|Y ) is a function of θ that shows how “likely” are various parameter values θ to have produced the data Y that were observed.For n = 1, the binomial distribution becomes the Bernoulli distribution. The mean value of a Bernoulli variable is = p, so the expected number of S’s on any single trial is p. More generally, suppose the probability of heads is p and we spin the coin n times. The probability that we get a total of k heads is given by the binomial distribution: for any value of k from 0 to n, including both. The term (n k) is the binomial coefficient, usually pronounced “n .
We now have two pieces of our Bayesian model in place – the Beta prior model for Michelle’s support \(\pi\) and the Binomial model for the dependence of polling data \(Y\) on \(\pi\): \[\begin{split} Y | \pi & \sim \text{Bin}(50, \pi) \ \pi & \sim \text{Beta}(45, 55). \ \end{split}\] Bayesian Inference is the use of Bayes theorem to estimate parameters of an unknown probability distribution. The framework uses data to update model beliefs, i.e., the distribution over the parameters of the model.
The binomial distribution is the PMF of k successes given n independent events each with a probability p of success. Mathematically, when α = k + 1 and β = n − k + 1, the beta distribution and the binomial distribution are related by [clarification needed] a factor of n + 1:
The following function computes the binomial distribution for given values of n and p: def make_binomial ( n , p ): """Make a binomial PMF. n: number of spins p: probability of heads returns: Series representing a PMF """ ks = np . arange ( n + 1 ) a = binom . .In Bayes' rule above we can see that the posterior distribution is proportional to the product of the prior distribution and the likelihood function: \begin{eqnarray} P(\theta | D) \propto P(D|\theta) P(\theta) \end{eqnarray}As we build up the equations, we'll put them together to create a generalized function for the binomial distribution. ***::: {#thm-permuation-example} #### Permuation Example for the Binomial Distribution - Each outcome we care about will have the *same* probability.Find the joint distribution of \(p\) and \(X\). Use R to simulate a sample of size 1000 from the joint distribution of \((p, X)\). From inspecting a histogram of the simulated values of \(X\), guess at the marginal distribution of \(X\). R Exercises. Simulating Multinomial Probabilities; Revisit Exercise 6.

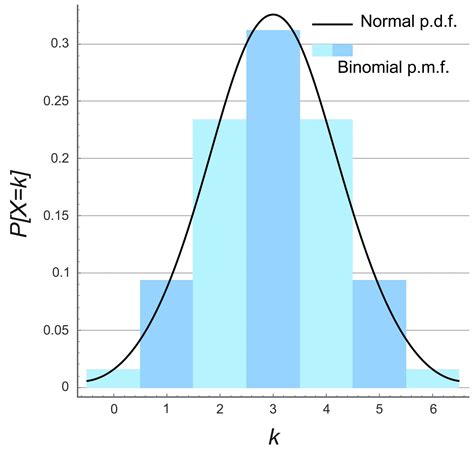
We will denote our posterior distribution for θ using p(θ|Y ). The likelihood function L(θ|Y ) is a function of θ that shows how “likely” are various parameter values θ to have produced the data Y that were observed.For n = 1, the binomial distribution becomes the Bernoulli distribution. The mean value of a Bernoulli variable is = p, so the expected number of S’s on any single trial is p. More generally, suppose the probability of heads is p and we spin the coin n times. The probability that we get a total of k heads is given by the binomial distribution: for any value of k from 0 to n, including both. The term (n k) is the binomial coefficient, usually pronounced “n .
We now have two pieces of our Bayesian model in place – the Beta prior model for Michelle’s support \(\pi\) and the Binomial model for the dependence of polling data \(Y\) on \(\pi\): \[\begin{split} Y | \pi & \sim \text{Bin}(50, \pi) \ \pi & \sim \text{Beta}(45, 55). \ \end{split}\]
binomial distribution statistics

binomial distribution probability
binomial distribution in math
beta and binomial distribution
As you can see a house’s architectural style does not limit the ability to choose from our black and white paint color ideas. White exterior houses, paired with some natural wood accents . See more
binomial distribution bayes box for p|binomial distribution statistics